Introduction to vimp
Brian D. Williamson
2025-09-25
Source:vignettes/introduction-to-vimp.Rmd
introduction-to-vimp.RmdIntroduction
vimp is a package that computes nonparametric estimates
of variable importance and provides valid inference on the true
importance. The package supports flexible estimation of variable
importance based on the difference in nonparametric
,
classification accuracy, and area under the receiver operating
characteristic curve (AUC). These quantities are all nonparametric
generalizations of the usual measures in simple parametric models (e.g.,
linear models). For more details, see the accompanying manuscripts Williamson, Gilbert, Carone, et al. (2020),
Williamson, Gilbert, Simon, et al. (2021),
and Williamson and Feng (2020).
Variable importance estimates may be computed quickly, depending on the techniques used to estimate the underlying conditional means — if these techniques are slow, then the variable importance procedure will be slow.
The code can handle arbitrary dimensions of features, and may be used to estimate the importance of any single feature or group of features for predicting the outcome. The package also includes functions for cross-validated importance.
The author and maintainer of the vimp package is Brian Williamson. The methods
implemented here have also been implemented in Python under the package
vimpy.
Installation
A stable version of the package may be downloaded and installed from
CRAN. Type the following command in your R console to install the stable
version of vimp:
install.packages("vimp")A development version of the package may be downloaded and installed
from GitHub using the devtools package. Type the following
command in your R console to install the development version of
vimp:
# only run if you don't have devtools
# previously installed
# install.packages("devtools")
devtools::install_github("bdwilliamson/vimp")Quick Start
This section should serve as a quick guide to using the
vimp package — we will cover the main functions for
estimating
-based
variable importance using a simulated data example. More details are
given in the next section.
First, load the vimp package:
Next, create some data:
# -------------------------------------------------------------
# problem setup
# -------------------------------------------------------------
# set up the data
set.seed(5678910)
n <- 1000
p <- 2
s <- 1 # desire importance for X_1
x <- data.frame(replicate(p, runif(n, -1, 1)))
y <- (x[,1])^2*(x[,1]+7/5) + (25/9)*(x[,2])^2 + rnorm(n, 0, 1)
# set up folds for hypothesis testing
folds <- sample(rep(seq_len(2), length = length(y)))This creates a matrix of covariates x with two columns,
a vector y of normally-distributed outcome values, and a
set of folds for a sample of n = 100 study
participants.
The workhorse function of vimp, for
-based
variable importance, is vimp_rsquared. There are two ways
to compute variable importance: in the first method, you allow
vimp to run regressions for you and return variable
importance; in the second method (discussed in “Using precomputed regression
function estimates in vimp”), you run the regressions
yourself and plug these into vimp. I will focus on the
first method here. The basic arguments are
- Y: the outcome (in this example,
y) - X: the covariates (in this example,
x) - indx: the covariate(s) of interest for evaluating importance (here, either 1 or 2)
- run_regression: a logical value telling
vimp_rsquaredwhether or not to run a regression of Y on X (TRUEin this example) - SL.library: a “library” of learners to pass to the function
SuperLearner(sincerun_regression = TRUE) - V: the number of folds to use for cross-fitted variable importance
This second-to-last argument, SL.library, determines the
estimators you want to use for the conditional mean of Y given X.
Estimates of variable importance rely on good estimators of the
conditional mean, so we suggest using flexible estimators and model
stacking to do so. One option for this is the SuperLearner
package; load that package using
library("SuperLearner")
# load specific algorithms
library("ranger")The code
est_1 <- vimp_rsquared(Y = y, X = x, indx = 1, run_regression = TRUE,
SL.library = c("SL.ranger", "SL.mean"), V = 2,
env = environment())uses the Super Learner to fit the required regression functions, and computes an estimate of variable importance for the importance of . We can visualize the estimate, standard error, and confidence interval by printing or typing the object name:
est_1## Variable importance estimates:
## Estimate SE 95% CI VIMP > 0 p-value
## s = 1 0.060945 0.04647807 [0.0130398, 0.2417368] FALSE 0.09488437
print(est_1)## Variable importance estimates:
## Estimate SE 95% CI VIMP > 0 p-value
## s = 1 0.060945 0.04647807 [0.0130398, 0.2417368] FALSE 0.09488437This output shows that we have estimated the importance of to be 0.061, with a 95% confidence interval of [0.013, 0.242].
Detailed guide
In this section, we provide a fuller example of estimating -based variable importance in the context of assessing the importance of amino acid sequence features in predicting the neutralization sensitivity of the HIV virus to the broadly neutralizing antibody VRC01. For more information about this study, see Magaret, Benkeser, Williamson, et al. (2019).
Often when working with data we attempt to estimate the conditional mean of the outcome given features , defined as .
There are many tools for estimating this conditional mean. We might choose a classical parametric tool such as linear regression. We might also want to be model-agnostic and use a more nonparametric approach to estimate the conditional mean. However,
- This involves using some nonparametric smoothing technique, which requires: (1) choosing a technique, and (2) selecting tuning parameters
- Naive optimal tuning balances out the bias and variance of the smoothing estimator. Is this the correct trade-off for estimating the conditional mean?
Once we have a good estimate of the conditional mean, it is often of scientific interest to understand which features contribute the most to the variation in . Specifically, we might consider where for a vector and a set of indices , denotes the elements of with index not in . By comparing to we can evaluate the importance of the th element (or group of elements).
Assume that our data are generated according to the mechanism . We define the population value of a given regression function as , where the numerator of this expression is the population mean squared error and the denominator is the population variance. We can then define a nonparametric measure of variable importance, which is the proportion of the variability in the outcome explained by including in our chosen estimation technique.
This document introduces you to the basic tools in vimp
and how to apply them to a dataset. I will explore one method for
obtaining variable estimates using vimp: you only specify a
library of candidate estimators for the conditional means
and
;
you allow vimp to obtain the optimal estimates of these
quantities using the SuperLearner (Laan, Polley, and Hubbard 2007), and use these
estimates to obtain variable importance estimates. A second method
(using precomputed estimates of the regression functions) exists and is
described in “Using precomputed
regression function estimates in vimp”.
A look at the VRC01 data
Throughout this document I will use the VRC01 data (Magaret, Benkeser, Williamson, et al. 2019), a subset of the data freely available from the Los Alamos National Laboratory’s Compile, Neutralize, and Tally Neutralizing Antibody Panels database. Information about these data is available here.
# read in the data
data("vrc01")While there are several outcomes of interest in these data
(continuous measures of neutralization and binary measures of
resistance), we will focus on the binary measure of resistance to VRC01
given by ic50.censored. This variable is a binary indicator
that the concentration of VRC01 necessary to neutralize 50% of viral
replicates in a sample (IC-50) was right-censored; since higher values
of IC-50 imply a more resistant virus, this indicator is a proxy for
viral resistance. In addition to the outcome of interest, there are
measurements on several groups of variables: viral subtype, geographic
region of origin (a potential confounding variable), amino acid sequence
features (further grouped into the CD4 binding sites, VRC01 binding
footprint, sites with sufficient exposed surface area, sites identified
as important for glycosylation, sites with residues that covary with the
VRC01 binding footprint, sites associated with VRC01-specific potential
N-linked glycosylation (PNGS) effects, sites in gp41 associated with
VRC01 neutralization or sensitivity, sites for indicating N-linked
glycosylation), region-specific counts of PNGS, viral geometry, cysteine
counts, and steric bulk at critical locations.
For the sake of simplicity, we will focus here on only three groups of features: viral subtype, geographic region of origin, and viral geometry features.
##
## Attaching package: 'dplyr'## The following objects are masked from 'package:stats':
##
## filter, lag## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, union
library("tidyselect")
# retain only the columns of interest for this analysis
y <- vrc01$ic50.censored
X <- vrc01 %>%
select(starts_with("geog"), starts_with("subtype"), starts_with("length"))Since there are 17 features and two groups, it is of interest to determine variable importance both for the individual features separately and for the two groups of features (since the geographic variables are potential confounders).
A first approach: linear regression
Suppose that I believe that a linear model truly describes the relationship between the outcome and the covariates in these data. In that case, I would be justified in only fitting a linear regression to estimate the conditional means; this means that in my importance analysis, I should also use only linear regression. The analysis is achieved by the following:
geog_indx <- max(which(grepl("geog", names(X))))
set.seed(1234)
for (i in seq_len(ncol(X) - geog_indx)) {
# note that we're using a small number of cross-fitting folds for speed
lm_vim <- vim(Y = y, X = X, indx = geog_indx + i, run_regression = TRUE, SL.library = "SL.glm", type = "r_squared", cvControl = list(V = 2), scale = "logit", family = binomial())
if (i == 1) {
lm_mat <- lm_vim
} else {
lm_mat <- merge_vim(lm_mat, lm_vim)
}
}
# print out the importance
lm_mat## Variable importance estimates:
## Estimate SE 95% CI VIMP > 0 p-value
## s = 5 0.01719729 0.06603158 [8.269615e-06, 0.9737017] FALSE 0.3972620
## s = 6 0.00000000 0.07069950 [0.000000e+00, 0.7222543] FALSE 0.9654196
## s = 7 0.00000000 0.07745084 [0.000000e+00, 0.7335209] FALSE 0.9563069
## s = 8 0.00000000 0.06708417 [0.000000e+00, 0.7063085] FALSE 0.9757243
## s = 9 0.00000000 0.07060735 [0.000000e+00, 0.7136383] FALSE 0.9708435
## s = 10 0.00000000 0.07109234 [0.000000e+00, 0.8783540] FALSE 0.8237980
## s = 11 0.00000000 0.06822808 [0.000000e+00, 0.6897041] FALSE 0.9838655
## s = 12 0.00000000 0.07302727 [0.000000e+00, 0.7693624] FALSE 0.9291195
## s = 13 0.00000000 0.06737901 [0.000000e+00, 0.6823319] FALSE 0.9870910
## s = 14 0.00000000 0.07578870 [0.000000e+00, 0.8869337] FALSE 0.8136219
## s = 15 0.00000000 0.07018926 [0.000000e+00, 0.8657089] FALSE 0.8373951
## s = 16 0.00000000 0.10191779 [0.000000e+00, 0.6167420] FALSE 0.9991101
## s = 17 0.00000000 0.08531226 [0.000000e+00, 0.7229246] FALSE 0.9620472
## s = 18 0.00000000 0.07551375 [0.000000e+00, 0.7170743] FALSE 0.9677898
## s = 19 0.00000000 0.07513031 [0.000000e+00, 0.9235423] FALSE 0.7718553
## s = 20 0.00000000 0.06632758 [0.000000e+00, 0.6743266] FALSE 0.9901541
## s = 21 0.00000000 0.07569105 [0.000000e+00, 0.9858755] FALSE 0.6724003Building a library of learners
In general, we don’t believe that a linear model truly holds.
Thinking about potential model misspecification leads us to consider
other algorithms. Suppose that I prefer to use generalized additive
models (Hastie and Tibshirani 1990) to
estimate
and
,
so I am planning on using the gam package. Suppose that you
prefer to use the elastic net (Zou and Hastie
2005), and are planning to use the glmnet
package.
The choice of either method is somewhat subjective, and I also will have to use a technique like cross-validation to determine an optimal tuning parameter in each case. It is also possible that neither additive models nor the elastic net will do a good job estimating the true conditional means!
This motivates using SuperLearner to allow the data to
determine the optimal combination of base learners from a
library that I define. These base learners are a combination of
different methods (e.g., generalized additive models and elastic net)
and instances of the same method with different tuning parameter values
(e.g., additive models with 3 and 4 degrees of freedom). The Super
Learner is an example of model stacking, or model aggregation — these
approaches use a data-adaptive combination of base learners to make
predictions.
For instance, my library could include the elastic net, random forests (Breiman 2001), and gradient boosted trees (Friedman 2001) as follows:
# create a function for boosted stumps
SL.gbm.1 <- function(..., interaction.depth = 1) SL.gbm(..., interaction.depth = interaction.depth)
# create GAMs with different degrees of freedom
SL.gam.3 <- function(..., deg.gam = 3) SL.gam(..., deg.gam = deg.gam)
SL.gam.4 <- function(..., deg.gam = 4) SL.gam(..., deg.gam = deg.gam)
SL.gam.5 <- function(..., deg.gam = 5) SL.gam(..., deg.gam = deg.gam)
# add more levels of alpha for glmnet
create.SL.glmnet <- function(alpha = c(0.25, 0.5, 0.75)) {
for (mm in seq(length(alpha))) {
eval(parse(file = "", text = paste('SL.glmnet.', alpha[mm], '<- function(..., alpha = ', alpha[mm], ') SL.glmnet(..., alpha = alpha)', sep = '')), envir = .GlobalEnv)
}
invisible(TRUE)
}
create.SL.glmnet()
# add tuning parameters for randomForest
create.SL.randomForest <- function(tune = list(mtry = c(1, 5, 7), nodesize = c(1, 5, 10))) {
tuneGrid <- expand.grid(tune, stringsAsFactors = FALSE)
for (mm in seq(nrow(tuneGrid))) {
eval(parse(file = "", text = paste("SL.randomForest.", mm, "<- function(..., mtry = ", tuneGrid[mm, 1], ", nodesize = ", tuneGrid[mm, 2], ") SL.randomForest(..., mtry = mtry, nodesize = nodesize)", sep = "")), envir = .GlobalEnv)
}
invisible(TRUE)
}
create.SL.randomForest()
# create the library
learners <- c("SL.glmnet", "SL.glmnet.0.25", "SL.glmnet.0.5", "SL.glmnet.0.75",
"SL.randomForest", "SL.randomForest.1", "SL.randomForest.2", "SL.randomForest.3",
"SL.randomForest.4", "SL.randomForest.5", "SL.randomForest.6", "SL.randomForest.7",
"SL.randomForest.8", "SL.randomForest.9",
"SL.gbm.1")Now that I have created the library of learners, I can move on to estimating variable importance.
Estimating variable importance for a single variable
The main function for R-squared-based variable importance in the
vimp package is the vimp_rsquared() function.
There are five main arguments to vimp_rsquared():
-
Y, the outcome -
X, the covariates -
indx, which determines the feature I want to estimate variable importance for -
SL.library, the library of candidate learners -
V, the number of cross-fitting folds (also referred to as cross-validation folds) to use for computing variable importance
The main arguments differ if precomputed regression function
estimates are used; please see “Using precomputed regression
function estimates in vimp” for further discussion of
this case.
Suppose that the first feature that I want to estimate variable
importance for is whether the viral subtype is 01_AE,
subtype.is.01_AE. Then supplying
vimp_rsquared() with
Y = yX = Xindx = 5SL.library = learnersV = 5
means that:
- I want to use
SuperLearner()to estimate the conditional means and , and my candidate library islearners - I want to estimate variable importance for the fifth column of the
VRC01 covariates, which is
subtype.is.01_AE - I want to use five-fold cross-fitting to estimate importance
The call to vimp_rsquared() looks like this:
vimp_rsquared(Y = y, X = X,
indx = 5, run_regression = TRUE, SL.library = learners, V = 5, family = binomial())While this is the preferred method for estimating variable importance, using a large library of learners may cause the function to take time to run. Usually this is okay — in general, you took a long time to collect the data, so letting an algorithm run for a few hours should not be an issue.
However, for the sake of illustration, I can estimate varibable importance for 01_AE subtype only using only using a small library, a small number of cross-validation folds in the Super Learner, and a small number of cross-fitting folds as follows (again, I suggest using a larger number of folds and a larger library in practice):
# small learners library
learners.2 <- c("SL.ranger")
# small number of cross-fitting folds
V <- 2
# small number of CV folds for Super Learner
sl_cvcontrol <- list(V = 2)
# now estimate variable importance
set.seed(5678)
start_time <- Sys.time()
subtype_01_AE_vim <- vimp_rsquared(Y = y, X = X, indx = 5, SL.library = learners.2, na.rm = TRUE, env = environment(), V = V, cvControl = sl_cvcontrol, family = binomial())
end_time <- Sys.time()This code takes approximately 0.986 seconds to run on a (not very fast) PC. I can display these estimates:
subtype_01_AE_vim## Variable importance estimates:
## Estimate SE 95% CI VIMP > 0 p-value
## s = 5 0.09860363 0.05610007 [0.03077091, 0.2737373] TRUE 0.03940455The object returned by vimp_rsquared() also contains
lists of fitted values from using SuperLearner(); I access
these using $full_fit and $red_fit. For
example,
head(subtype_01_AE_vim$full_fit[[1]])## [1] 0.05702815
head(subtype_01_AE_vim$red_fit[[1]])## [1] 0.06298279I can obtain estimates for the remaining individual features in the same way (again using only using a small library for illustration):
ests <- subtype_01_AE_vim
set.seed(1234)
for (i in seq_len(ncol(X) - geog_indx - 1)) {
# note that we're using a small number of cross-fitting folds for speed
this_vim <- vimp_rsquared(Y = y, X = X, indx = geog_indx + i + 1, run_regression = TRUE, SL.library = learners.2, V = V, cvControl = sl_cvcontrol, family = binomial())
ests <- merge_vim(ests, this_vim)
}Now that I have estimates of each of individual feature’s variable importance, I can view them all simultaneously by plotting:
library("ggplot2")
library("cowplot")
theme_set(theme_cowplot())
all_vars <- c(paste0("Subtype is ", c("01_AE", "02_AG", "07_BC", "A1", "A1C", "A1D",
"B", "C", "D", "O", "Other")),
paste0("Length of ", c("Env", "gp120", "V5", "V5 outliers", "Loop E",
"Loop E outliers")))
est_plot_tib <- ests$mat %>%
mutate(
var_fct = rev(factor(s, levels = ests$mat$s,
labels = all_vars[as.numeric(ests$mat$s) - geog_indx],
ordered = TRUE))
)
# plot
est_plot_tib %>%
ggplot(aes(x = est, y = var_fct)) +
geom_point() +
geom_errorbarh(aes(xmin = cil, xmax = ciu)) +
xlab(expression(paste("Variable importance estimates: ", R^2, sep = ""))) +
ylab("") +
ggtitle("Estimated individual feature importance") +
labs(subtitle = "in the VRC01 data (considering only geographic confounders, subtype, and viral geometry)")## Warning: `geom_errobarh()` was deprecated in ggplot2 4.0.0.
## ℹ Please use the `orientation` argument of `geom_errorbar()` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.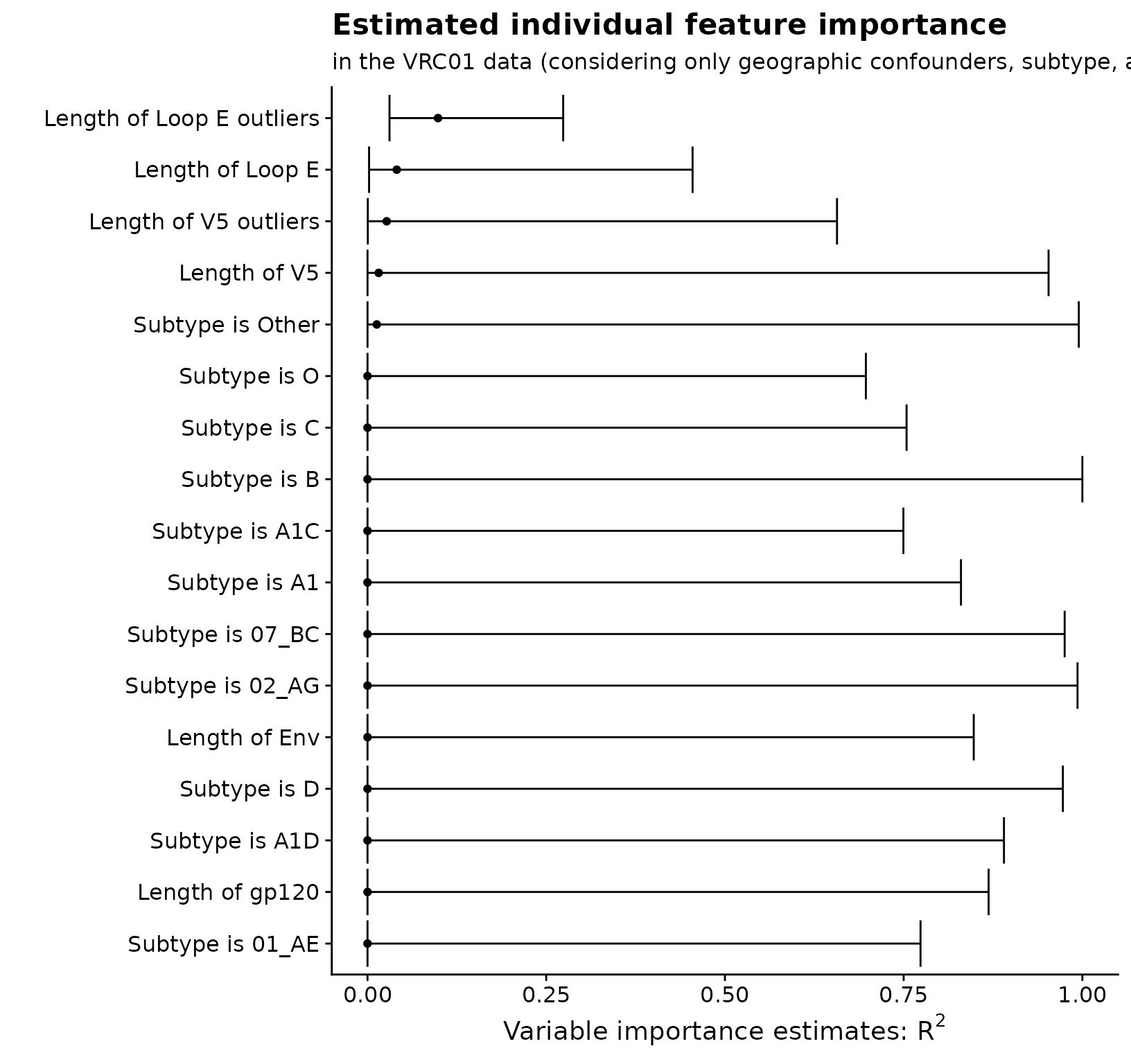
Estimating variable importance for a group of variables
Now that I have estimated variable importance for each of the individual features, I can estimate variable importance for each of the groups that I mentioned above: biological and behavioral features.
The only difference between estimating variable importance for a
group of features rather than an individual feature is that now I
specify a vector for s; I can use any of the options listed
in the previous section to compute these estimates.
# get the estimates
set.seed(91011)
subtype_vim <- vimp_rsquared(Y = y, X = X, indx = 5:15, SL.library = learners.2, na.rm = TRUE, env = environment(), V = V, cvControl = sl_cvcontrol, family = binomial())## Warning in cv_vim(type = "r_squared", Y = Y, X = X, cross_fitted_f1 =
## cross_fitted_f1, : Original estimate < 0; returning zero.
geometry_vim <- vimp_rsquared(Y = y, X = X, indx = 16:21, SL.library = learners.2, na.rm = TRUE, env = environment(), V = V, cvControl = sl_cvcontrol, family = binomial())
# combine and plot
groups <- merge_vim(subtype_vim, geometry_vim)
all_grp_nms <- c("Viral subtype", "Viral geometry")
grp_plot_tib <- groups$mat %>%
mutate(
grp_fct = factor(case_when(
s == "5,6,7,8,9,10,11,12,13,14,15" ~ "1",
s == "16,17,18,19,20,21" ~ "2"
), levels = c("1", "2"), labels = all_grp_nms, ordered = TRUE)
)
grp_plot_tib %>%
ggplot(aes(x = est, y = grp_fct)) +
geom_point() +
geom_errorbarh(aes(xmin = cil, xmax = ciu)) +
xlab(expression(paste("Variable importance estimates: ", R^2, sep = ""))) +
ylab("") +
ggtitle("Estimated feature group importance") +
labs(subtitle = "in the VRC01 data (considering only geographic confounders, subtype, and viral geometry)")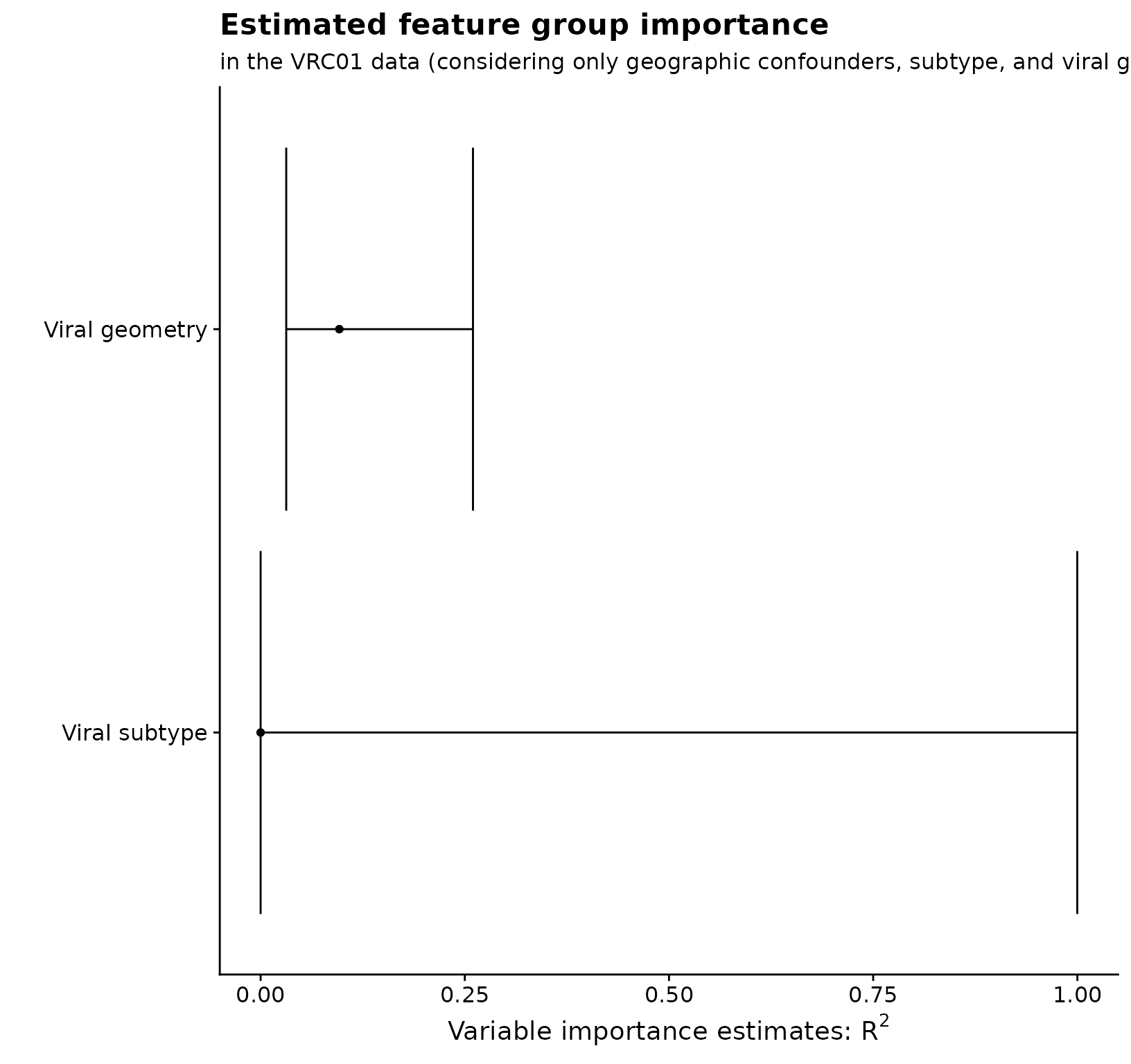
Types of population variable importance
In this document, I have focused on one particular definition of population variable importance that I call conditional variable importance. For a further discussion of what I call marginal variable importance and Shapley population variable importance, please see “Types of VIMs”.